로지스틱 회귀

종속 변수와 독립 변수 간의 관계를 구체적으로 나타냄 

-> 향후 예측 모델에 사용

 

연속된 값을 예측하지 않고 종속 변수가 범주형 데이터일 때 사용

-> 결과 특정 카테고리로 분류됨

 

회귀를 사용하여 범주에 속할 확률 예측

-> 가능성이 더 높은 범주로 분류하는 머신러닝 지도 학습 알고리즘

 

로지스틱 함수를 이용하여 분류

 

 

이항 로지스틱 회귀 

종속 변수가 2개인 binary 형태

-> 날씨 (hot, cold)

 

다항 로지스틱 회귀 

종속 변수가 3개 이상인 multi 형태일 때

-> 날씨 (rainy, sunny, cloudly)

 

시그모이드 함수

Y값 범위의 제한 

다양한 변형 가능

실제 존재 하는 경우의 함수

모든 X값에 대응

증가함수 사후확률 변환 인지가 쉬움

인공 뉴런의 활성화 함수로 사용

 

로지스틱 함수

0 < odds < 양의 무한대 범위에 속해서 범위의 제약 존재

확률 값과 odds 값은 비대칭성

음의 무한대부터 양의 무한대 범위를 만들기 위해 로그 취하기

로지트 함수는 로지스틱(시그모이드) 함수의 역함수 

 

성장 곡선에서 자주 사용

시그모이드 함수 성질 보유

미분값 쉽게 계산 가능
-> 최적화하여 극점 통해 계산

 

손실 함수

Y = 0 , Y = 1 일때.

 

경사하강법

선형 회귀와 같이 경사하강법을 사용

-> 모든 데이터에서 로그 손실을 최소화하는 계수를 찾기 가능

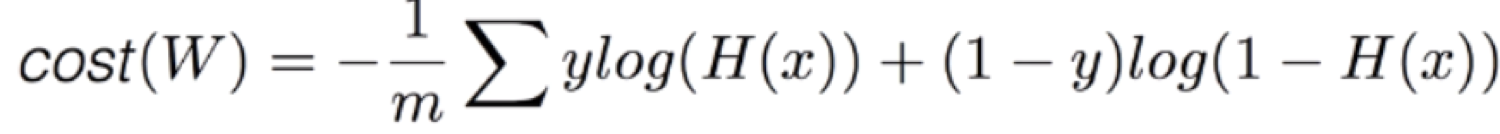
임계값

모델의 민감도를 높일 필요가 존재

-> 임계값 낮추기 

ex) 암 진단 모델

 

코드 예제 실습

#로지스틱 회귀 이용하여 데이터 학습
#데이터 학습 후, 앞에 있는 데이터 30개 따로 추출
#값을 해당 모델을 이용해 예측
#시각화

lr = LogisticRegression().fit(x, y)
test_x = x[:30]
test_y = lr.predict(test_x[:, :])

for i in range(30):
	if test_y[i] == 0:
    	plt.scatter(test_x[i:i+1, 0], test_x[i:i+1, 1], c='red')
    else:
    	plt.scatter(test_x[i:i+1, 0], test_x[i:i+1, 1], c='blue')
        
print(lr.coef_. lr.intercept_)
x1, y1 = [-lr.intercept_ / lr.coef_[0][0], (-lr.intercept_ -lr.coef_[0][1]*100) / lr.coef_[0][0]], [0, 100]
plt.plot(x1, y1m color='black')
plt.show()